熟悉的原因是,在分解因式时我们经常用到十字相乘法;陌生的原因是,我们仅仅熟悉二次项系数为“1”的十字相乘法,对于二次项系数不为“1”,及双十字相乘法法知之甚少,或者无从下手。
本文将针对以上问题,把十字相乘法做具体的阐述。
先来看知识要点:
在了解十字相乘法前先来理解下什么是二次三项式:
二次三项式:多项式ax^2+bx+c,称为字母x的二次三项式,其中ax^3称为二次项,bx为一次项,c为常数项.
1.十字相乘法的依据:
利用十字相乘法分解因式,实质上是逆用多项式的乘法法则。
如在多项式乘法中有:(x+a)(x+b)=x^2+(a+b)x+ab
反过来可得:x^2+(a+b)x+ab=(x+a)(x+b)
2.十字相乘法的定义:
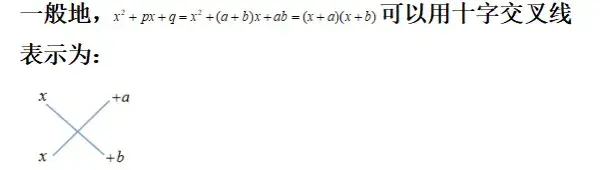
利用十字交叉线来分解系数,把二次三项式分解因式的方法叫做十字相乘法.
3.能用十字相乘法分解的多项式的特征:
(1)必须是一个二次三项式;
(2)二次三项式的系数为1时,常数项能分解成两个因数和的积,且这两个因数的和正好等于一次项系数,这种方法的特征是“拆常数项,凑一次项”;
(3)对于二次项系数不是1的二次三项式,一般要借助“画十字交叉线”的办法来确定.
4.用十字相乘法因式分解的符号规律
(1)当常数项是“+”号时,分解的两个一次二项式中间同号;
(2)当常数项是“”号时,分解的两个一次二项式的因式中间是异号;
(3)当二次项系数为负数时,先提出负号,使二次项系数为正数,然后再看常数项.
5.用十字相乘法分解二次项系数不为1的二次三项式:

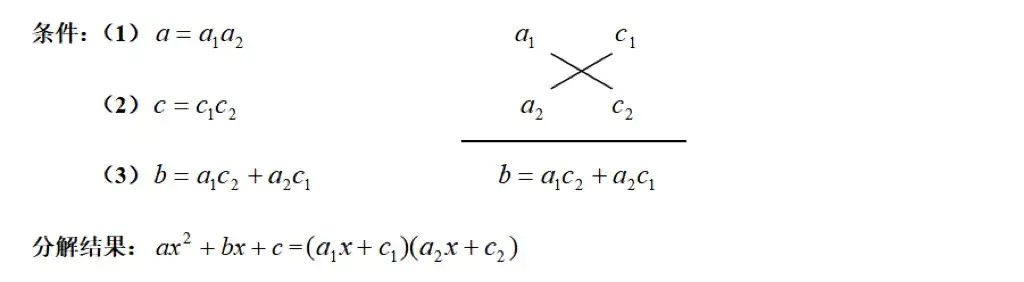
来看道例题,加深下理解:

十字相乘法,可以概括为 16 个字:“头尾分解,交叉相乘,求和凑中,横向写出”
6.双十字相乘法:
双十字相乘法也叫作“长十字相乘法”,它一般适用于二元二次六项式。形如:Ax^2+Bxy+Cy^2+Dx+Ey+F的多项式因式分解。
主要步骤:
(1)运用十字相乘法分解前三项组成的二次三项式;
(2)在这个十字相乘图的右边再画一个十字,把常数项分解为两个因数,填在第二个十字的右端,使这两个因数与含y项的交叉之积的和等于原多项式中含y的一次项Ey,同时这两个因数与含x的项的交叉之积的和等于原多项式中含x的一次项Dx.
通过一道例题再来理解下:
例:分解因式:x^2+xy-2y^2+5y-2x-3

相同颜色的十字和系数一一对应
注意‼️式中的三个十字叉实际是三次十字相乘.如果剩余项系数验证失败,可以把同一列的两个数的位置交换一下,或者重新拆分再验证.
最后来看20道典型例题,及时巩固、举一反三。

